基于FPGA的格密码关键运算模块的设计与实现*

韩炼冰，房利国，王 松，刘鸿博，杨敏旭

（中国电子科技集团公司第三十研究所，四川 成都 610041）

随着量子计算技术的发展，量子计算机将能在人们可以接受的时间内破解许多目前计算机无法破解的密码，其中就包括目前大部分公钥密码系统所依赖的大整数质数拆分问题和离散对数问题这两大数学难题。

为应对量子计算机为传统密码系统带来的挑战，后量子密码[1]已成为国内外众多学者的重点研究对象。2016年，美国国家标准与技术研究院（Nation Institute of Standards and Technology，NIST）开始了一项针对抗量子密码系统的征集计划，旨在寻找、设计、开发和标准化抗量子密码系统，以便于在未来取代现有的密码系统标准。经过3轮的征集提交和筛选，2022年7月NIST发布了首批入围标准的4个抗量子算法：Crystals-kyber、CRYSTALSDILITHIUM、FALCON和SPHINCS+。这4个算法中有3个基于格的数学难题，另一个使用了散列函数。由此可见，基于格的密码方案是抗量子计算密码学中的研究热点。基于格的密码算法中的运算大多为线性运算，因此较其他密码系统，基于格的密码系统具有计算速度快[2]、密钥和密文较小等优势[3]。本文对格密码中的关键模块——多项式乘法进行研究，给出了一种多项式乘法的运算方法和硬件实现架构，并在现场可编程门阵列（Field Program Gate Array，FPGA）中进行了实现和评估，为格密码硬件实现提供参考。

1.1 格密码数学基础

线性独立空间上有集合v1,v2,…,vn∈Rn，格就是这些向量的线性组合，这一过程的表达式为：

式中：系数a均在整数域Z中。任意一组可以生成格的线性无关向量都称为格的基，格的维度等于格的基中的向量个数。

目前常用的两个基于格的困难问题是短整数问题（Shortest Integer Problem，SIS）和错误学习问题（Learning With Error，LWE），但基于上述两个问题的加密方案需要的密钥量大、效率低、资源消耗高，无法在实际中运用。因此，Lyubashevsky等人[4]在LWE的基础上提出了环上错误学习（Ring Learning With Errors，RLWE）问题。基于RLWE的加密方案在性能上有着显著的优势[5]，这是现在许多格密码算法的理论基础。RLWE在环Zq[x]=f上进行操作，其中f是n项的不可约多项式，通常f=xn+1，其中n是2的幂，q为素数。

1.2 环多项式乘法

对于RLWE密码算法，其中最为耗时的是环多项式乘法。环多项式乘法有两种实现方式[6-7]，分别为经典乘法和快速数论变换（Number Theoretic Transform，NTT）乘法。

1.2.1 经典乘法

经典乘法先把多项式a中的每一项与多项式b中的每一项相乘，再把每个多项式相加得到最终结果。如果多项式a和b的最高次项都为n-1，那么计算复杂度为O(n2)，需要n2个乘法和(n-1)2个加减法。

1.2.2 NTT乘法

NTT是基于快速傅里叶变换（Fast Fourier Transform，FFT）实现的，其将FFT中的旋转因子由复数变成了整数。设正整数序列x(n)，其所有元素均小于模数M，有如下NTT变换[8]：

式（2）为NTT正变换，式（3）为逆NTT变换。其中，a为模M的N阶本原单位根，满足：

amn是a-mn在模M下的逆元，满足以下性质：

NTT运算是一个递推的过程，图1给出了N=8点的NTT运算结构。如图1中的椭圆标识所示，NTT变换后的结果顺序与原输入顺序呈二进制的倒序关系，因此为避免在计算完成后进行顺序变换，通常采用逆序的方式进行运算，运算结构如图2所示。图3为一次蝶形运算。N通常可以表示为2的幂的形式，N=2L，则N点NTT运算需要执行次蝶形运算，所以8点NTT需要执行12次蝶形运算。

图1 8点NTT运算结构

图2 8点NTT逆序运算结构

图3 蝶形运算a

2.1 多项式乘法算法

NTT中的每一次蝶形运算都需要做一次乘法和乘法结果取模运算，因此快速完成乘法和取模运算是提高NTT运算效率的关键。本文采用了Longa等人[9]提出的适用于模数M=k2p+1的高效取模算法，即LN取模算法，再结合FPGA内部的高效乘法器来实现NTT快速运算。

LN取模算法有K-RED和K-RED2x两种形式[10]，如算法1和算法2所示。算法1适用于对加法结果取模，算法2适用于对乘法结果取模。

NTT变换和逆NTT变换算法如下：

算法3中M为模数，g为单位根，N为多项式的项数，如果N不满足2的整数次幂需要补0。步骤6-9为一次蝶形运算。步骤11正变换查t1，逆变换查t2。

算法4中的步骤7每运算一次相当于在该项上乘以了k，步骤8每运算一次相当于在该项上乘以k2，如果对步骤8中每个gg都乘以k-1，经过步骤8运算后也相当于该项上乘以k。NTT每一项的运算次数为算法4中步骤2总的循环次数，即log2N次（N为多项式的项数）。所以每项都增加了klog2N倍，增加部分可以通过预计算的方式消除。

算法5中的步骤1是为了消除NNT运算时每项增加的klog2N倍而做的预处理。步骤6中的k-(4+log2N)N-1则是为了消除INNT运算后扩大的klog2N倍，并完成INNT运算后的除法运算。

2.2 多项式乘法FPGA实现

多项式乘法的FPGA实现如图4所示。

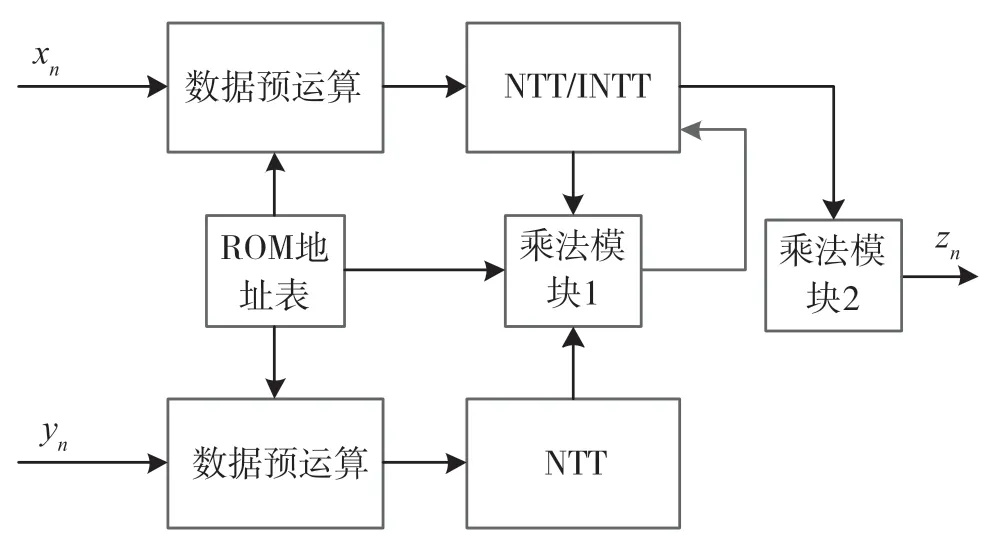
图4 多项式乘法FPGA实现

2.2.1 数据预运算模块

数据预运算模块用于对多项式数据进行预处理，同时完成对多项式的倒位序。ROM地址表内存放预计算好的位序映射表。根据ROM读出的地址读取原始序列，预运算后写入NTT模块内的存储器中。

2.2.2 NTT模块

图5为NTT模块的实现。

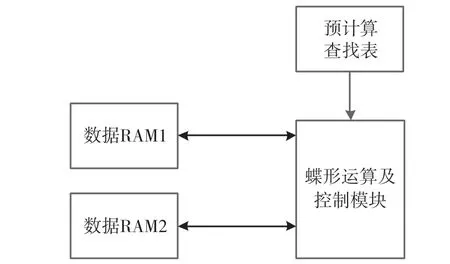
图5 NTT实现

数据RAM1和数据RAM2为多项式系数存储区，由于FPGA内部实现的RAM通常只有2路通道，不能满足蝶形运算同时对RAM的2次读和写操作。为了解决这个问题，本文设计了RAM1和RAM2两个数据存储区。当RAM1作为数据读取区时，蝶形运算的结果写入RAM2区，当RAM2作为数据读取区时，蝶形运算的结果写入RAM1区，由内部控制模块乒乓切换两个数据区的读写模式。

预计算查找表用于存放蝶形运算所需的预计算数据，该数据可以预先计算好后固化在存储区内部，不占用NTT的计算时间。预计算的数据包括k-1ai，k-1a-i，k-(2+log2N)和k-(4+log2N)N-1。

蝶形运算及控制模块通过状态机控制NTT的3层循环，以及每次蝶形数据和预计算数据的读取，调用K-RED和K-RED2x完成运算。因蝶形运算下一次的输入数据不会用到上一次的结果，所以蝶形运算可实现流水操作，从而提升运算性能。

2.2.3 乘法模块

乘法模块用于完成算法5的步骤4和步骤6。其中乘法模块1用于完成两个多项式转换到NTT域后各项的相乘，并根据ROM地址表内存放的地址读取多项式的值相乘，将结果存放在NNT的RAM内，用于逆NNT运算。乘法模块2用于完成逆NTT运算结果除N运算和消除K-RED2x运算产生的k2缩放。由于k通常都不大，K-RED2x内部的k2x0和kx1可以转换为由移位和加法实现，不需要乘法运算。

为了便于结果评估，本文选用模数M=12 289，并设多项式的项数N=1 024，测试平台采用Xilinx公司的XC7K325T型号FPGA。

Kuo等人[11]运用了适合于硬件实现的模约减方法，但使用了较多的加法器，编译频率不高。Oder等人[12]使用的模约减模块包含延时较大的关键路径，且存取效率不高，编译频率也较低。本文的蝶形运算模块及LN模运算模块均采用流水线实现，所以实现频率较高，达到了320 MHz。由于采用流水实现，预算模块和NTT运算可以并行执行，且NTT内部的蝶形运算模块同样为流水结构，从而大大提高了运算性能。表1为本文多项式乘法硬件实现与现有一些硬件实现的比较结果。其中，查找表（Look-Up-Table，LUT）、寄存器（REGister，REG）、块存储器（Block RAM，BRAM）和乘法器（Digital Signal Processing，DSP）分别为FPGA内硬件资源。

表1 多项式乘法硬件评估结果

本文提出的多项式乘法硬件实现方法，采用不完全模约减的方式取模，大大减少了取模的时间。同时采用了乒乓切换、流水技术和双NTT模块架构，一方面提高了存储器读写带宽，另一方面减少了运算过程中的等待时间，从而提升了运算性能。此外，由于采用了流水设计，编译主频也较高，达到了320 MHz。因此，本设计无论是在资源占用方面还是在处理性能方面都具有一定的优势，对基于格的后量子密码的硬件实现具有一定的参考意义。

猜你喜欢蝶形乘法量子算乘法小学生学习指导(低年级)(2022年10期)2022-11-05蝶形引入光缆技术新进展光通信研究(2022年2期)2022-03-29《量子电子学报》征稿简则量子电子学报(2022年1期)2022-02-25我们一起来学习“乘法的初步认识”数学小灵通(1-2年级)(2021年10期)2021-11-05蝶形腹板剪切变形计算与分析苏州科技大学学报(工程技术版)(2021年2期)2021-07-02《整式的乘法与因式分解》巩固练习语数外学习·初中版(2020年11期)2020-09-10决定未来的量子计算小学科学(学生版)(2020年1期)2020-01-19把加法变成乘法小学生学习指导(低年级)(2019年9期)2019-09-25新量子通信线路保障网络安全科学大众（中学）(2019年2期)2019-04-08一种简便的超声分散法制备碳量子点及表征西安工程大学学报(2016年6期)2017-01-15